The interesting book Spiral: Origami | Art | Design by Tomoko Fuse contains an entire chapter devoted to spirals made of a succession of similar polygons.
I folded one of these models to obtain the result of Figure 1.
Figure 1. Triangular spiral
It is interesting to note that this model is an example of what is known in mathematics as "proof without words". Let me explain better!
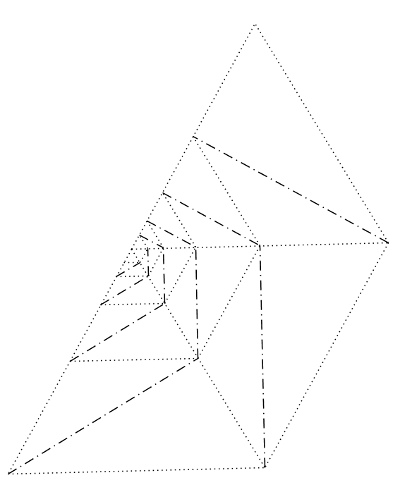
Figure 2.
In Figure 2, I reproduced with GeoGebra the succession of triangles of the origami model. If we assume that the area of the initial equilateral triangle is unitary. Then, the areas of the different triangles appearing in the picture follow a geometric progression of common ratio 1/4.
It is well known that
So Figure 2 "makes visible" and intuitive these facts and it can be used to introduce the idea of series at an elementary level.
From an origamistic point of view it is interesting to underline that the model is folded starting from a preprinted crease pattern which contains only mountain and valley folds.
Figure 3. Crease pattern of the origami model
I have created the crease pattern with GeoGebra, but it could be a good exercise in programming to do the same writing a PostScript code!



I programmed figure 2 in Sage. You can change the number of iterations on the last line: http://lazza.me/Vy4Y1F
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteVery nice result :-)
ReplyDelete